Что такое аппроксимация, интерполяция и экстраполяция

Пример реализации

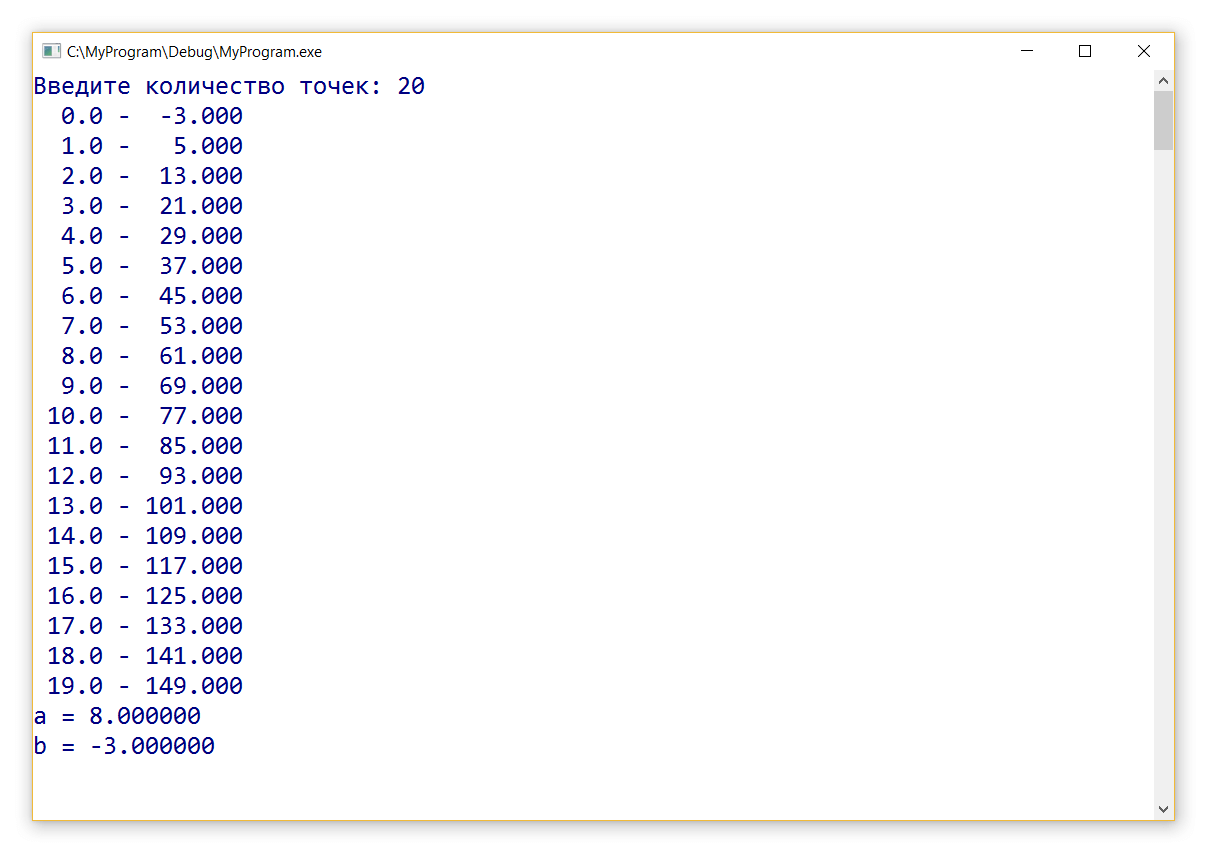
Для примера реализации воспользуемся набором значений, полученных в соответствии с уравнением прямой

y = 8 · x — 3

Рассчитаем указанные коэффициенты по методу наименьших квадратов.
Результат сохраняем в форме двумерного массива, состоящего из 2 столбцов.
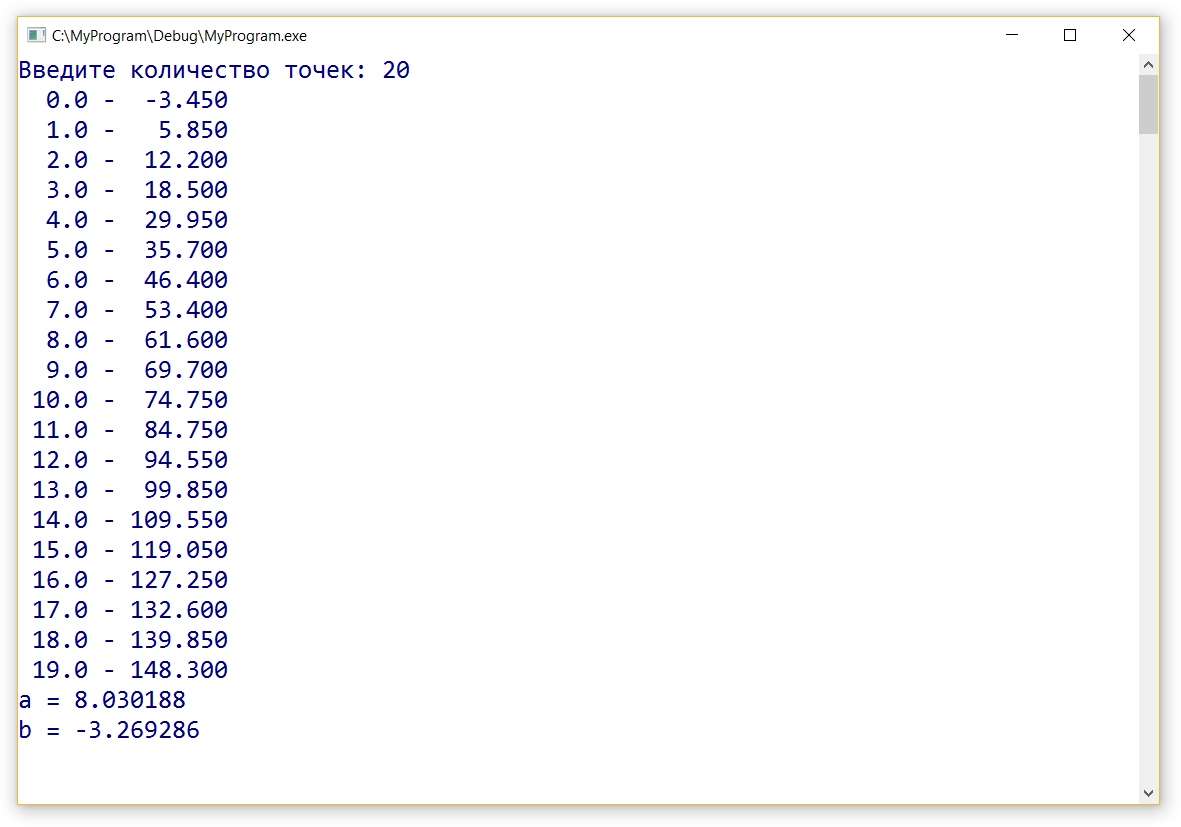
При следующем запуске программы добавим случайную составляющую к указанному набору значений и снова рассчитаем коэффициенты.Реализация на Си

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748

#define _CRT_SECURE_NO_WARNINGS#include <stdio.h>#include <stdlib.h>// Задание начального набора значенийdouble ** getData(int n) {  double **f;  f = new double*;  f = new double;  f = new double;  for (int i = 0; i<n; i++) {    f = (double)i;    f = 8 * (double)i — 3;    // Добавление случайной составляющей    f = 8*(double)i — 3 + ((rand()%100)-50)*0.05;  }  return f;}// Вычисление коэффициентов аппроксимирующей прямойvoid getApprox(double **x, double *a, double *b, int n) {  double sumx = 0;  double sumy = 0;  double sumx2 = 0;  double sumxy = 0;  for (int i = 0; i<n; i++) {    sumx += x;    sumy += x;    sumx2 += x * x;    sumxy += x * x;  }  *a = (n*sumxy — (sumx*sumy)) / (n*sumx2 — sumx*sumx);  *b = (sumy — *a*sumx) / n;  return;}int main() {  double **x, a, b;  int n;  system(«chcp 1251»);  system(«cls»);  printf(«Введите количество точек: «);  scanf(«%d», &n);  x = getData(n);  for (int i = 0; i<n; i++)    printf(«%5.1lf — %7.3lf\n», x, x);  getApprox(x, &a, &b, n);  printf(«a = %lf\nb = %lf», a, b);  getchar(); getchar();  return 0;}

Определение и смысл термина

Аппроксимация — это математическая процедура получения аналитической (или численной) функции, которая аппроксимирует (приближает) значения другой функции. Эта функция может быть использована для описания поведения первоначальной функции в различных точках области определения.

Слово «аппроксимация» происходит от латинского слова «approximatus», что переводится как «быть близко». Таким образом, аппроксимация позволяет нам приближенно описывать сложные функции и спрогнозировать их поведение в будущем.

Аппроксимация широко используется в физике, экономике, статистике, инженерии и других областях, где требуется описать и предсказать поведение систем. Например, для определения потерь сигнала в проводниках, аппроксимация мощности зависимости от расстояния может быть использована для прогнозирования, как много мощности может быть передано через проводник на определенном расстоянии.

Существует множество методов аппроксимации, включая полиномиальную, кусочно-линейную, нелинейную регрессию, кривые наименьших квадратов и другие. Выбор метода зависит от цели аппроксимации и характеристик данных.

Определение аппроксимации

Аппроксимация — это метод приближенного представления сложных функций или объектов с помощью более простых и понятных моделей или аппаратуры. Она часто используется в науке, инженерии, компьютерной графике и других областях.

Цель аппроксимации — приблизить сложные объекты или функции с добавлением погрешности, чтобы упростить их изучение, анализ или решение задач. Аппроксимация позволяет сэкономить время и ресурсы, которые могли бы понадобиться для точного описания или воспроизведения объекта или функции.

В процессе аппроксимации используются различные методы и модели, в зависимости от требуемой точности и сложности аппроксимируемого объекта или функции. Некоторые из наиболее распространенных методов аппроксимации включают интерполяцию, аппроксимацию регрессионными моделями, приближенные вычисления и т.д.

Пожалуйста, аппроксимация — это приближенное представление сложных объектов или функций с помощью более простых моделей или методов. Она позволяет упростить анализ и решение задач, сэкономить ресурсы и сократить время, которое могло бы быть затрачено на точное описание или воспроизведение объекта или функции.

Простое объяснение аппроксимации

Объясните, проще, пожалуйста!

Аппроксимация — это метод, который позволяет нам приблизительно представить сложную или неизвестную функцию или данные с помощью более простой функции или модели.

Когда у нас есть большой объем данных или сложная математическая функция, бывает трудно работать с ними напрямую. В таких случаях аппроксимация приходит на помощь!

Мы можем выбрать более простую функцию или модель, которая имеет похожую форму или свойства, как у наших данных или сложной функции. С помощью аппроксимации мы можем использовать эту упрощенную модель для анализа данных или решения задачи.

Например, представьте, что у нас есть график с множеством точек, которые представляют значения температуры каждый час в течение суток. Это много точек, и мы хотим сделать прогноз, какая будет температура в определенный момент времени. Вместо того чтобы работать с каждой точкой, мы можем использовать аппроксимацию для построения гладкой кривой, которая представляет общий тренд изменения температуры. Тогда мы можем использовать эту кривую для прогнозирования температуры в будущем без необходимости анализировать каждую точку отдельно.

Аппроксимация очень полезна, когда у нас есть ограниченное количество данных или когда мы хотим сократить объем вычислений для упрощения анализа. Этот метод широко применяется в различных научных и инженерных областях, таких как физика, экономика, статистика и многих других.

В итоге, аппроксимация помогает нам приблизительно представить сложные данные или функции с помощью более простых моделей или функций, чтобы облегчить их анализ или использование для решения задач.

Аппроксимация в математике

Аппроксимация — это метод математического моделирования, позволяющий приближенно описать сложные или неизвестные функции или данные. Она основана на использовании более простых и понятных моделей.

Аппроксимация в математике может быть полезна для решения различных задач. Например, если у вас есть множество точек данных, вы можете использовать аппроксимацию, чтобы найти более простое уравнение или функцию, которая близко приближается к вашим данным.

Проще говоря, аппроксимация позволяет нам упростить сложные данные или функции, чтобы мы могли лучше понять их или использовать их для дальнейших расчетов.

Существует несколько различных методов аппроксимации, таких как метод наименьших квадратов, интерполяция, аппроксимация по Чебышеву и многие другие.

Метод наименьших квадратов — один из самых распространенных методов аппроксимации, который позволяет найти наилучшую аппроксимирующую функцию, минимизируя сумму квадратов разностей между значениями функции и данными точками.

Интерполяция — это метод аппроксимации, позволяющий нам получить промежуточные значения между заданными точками данных. Например, если у вас есть две точки, вы можете использовать интерполяцию, чтобы найти значения между ними.

Аппроксимация по Чебышеву — это метод, который позволяет найти аппроксимацию функции наилучшим образом, используя чебышевские полиномы. Этот метод является очень эффективным и широко применяется в различных областях, включая численное моделирование и интерполяцию функций.

Все эти методы аппроксимации позволяют нам упростить сложные данные или функции, чтобы мы могли лучше понять и использовать их. Они находят широкое применение в различных областях науки и техники, таких как физика, экономика, инженерия и многие другие.

Применение аппроксимации в расчетах и моделировании

Аппроксимация – это математический метод, который заключается в приближении сложной функции более простой или известной функцией. Этот метод широко используется в расчетах и моделировании различных процессов в науке и технике. Рассмотрим, как применение аппроксимации помогает в решении различных задач.

Расчет функции

Когда нам нужно расчитать значение функции для большого количества точек, использование сложной функции может быть очень медленным и затратным. В таких случаях мы можем использовать метод аппроксимации, чтобы приблизительно оценить результат и ускорить вычисления.

Моделирование процесса

При моделировании процесса мы часто сталкиваемся с задачей описания его поведения с помощью математических формул. Однако, не всегда удастся найти формулу, которая полностью описывает идеальное поведение. В таком случае аппроксимация может помочь приблизительно описать процесс и получить решение.

Обработка сигналов

Аппроксимация также используется в обработке сигналов, например, в цифровой обработке речи. В этом случае мы можем использовать алгоритмы аппроксимации, чтобы преобразовать речь в сигналы, которые могут быть обработаны с помощью цифровых методов.

Таким образом, применение аппроксимации имеет множество практических применений в науке и технике. Она позволяет эффективно вычислять функции, моделировать процессы и обрабатывать сигналы.

Экстраполяция. Экстремально за пределами

Экстраполяция — нахождение значений за пределами интервала. До этого мы искали промежуточные значения на графике. Теперь представим еще одну ситуацию. График заканчивается, мы узнали текущие значения, и надо предположить, какие значения этот же показатель будет принимать в будущем. 

Получается задача прогнозирования, одна из ключевых в науке о данных. Для ее решения математика предлагает методы экстраполяции. Разница с интерполяцией в том, что неизвестные данные ищутся не в промежутке, а за его пределами.

Красные точки на графике высчитаны с помощью экстраполяции:

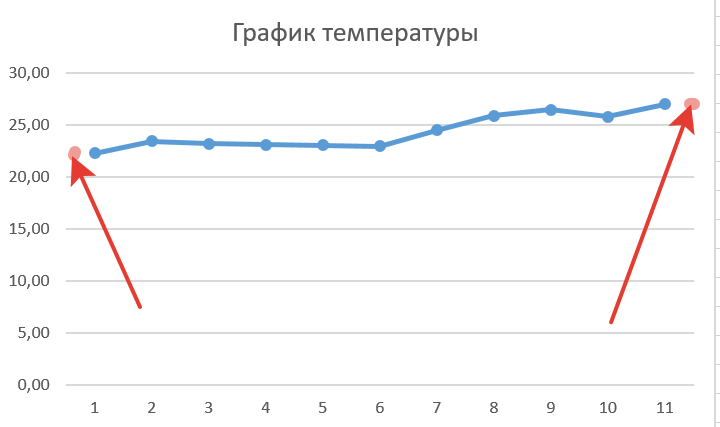
Мы не знаем, какими они были или будут на самом деле. Но можем рассчитать благодаря численным методам.

Как и в случае с интерполяцией, существует огромное количество методов для расчета. Некоторые из них дублируют интерполирующие методы. Например, популярный способ — параболическая экстраполяция, которую считают с помощью формул интерполяции.

Зачем это нужно. Для решения задачи прогнозирования и получения большего количества данных. И наоборот — для ретроспективного прогнозирования, чтобы понять примерные результаты из прошлого, еще до начала отслеживания.

Как связано с другими методами. Как и с интерполяцией, экстраполяцию удобнее проводить на аппроксимированных кривых. Для экстраполирования используются многие формулы и методы, которые обычно применяют при интерполяции данных.

Принципы аппроксимации и их роль в науке

Аппроксимация — это процесс приближения сложной функции или явления более простой моделью или функцией, которая дает приемлемую точность при решении задачи. Принципы аппроксимации широко используются в науке, в том числе в физике, математике, экономике и других областях.

1. Принцип упрощения: В основе аппроксимации лежит идея упрощения сложных явлений до более простых моделей. Это позволяет исследователям увидеть основные закономерности и взаимосвязи, которые в противном случае могли бы остаться незамеченными. Принцип упрощения помогает сделать сложное понятным и обеспечивает возможность анализа и прогнозирования.

2. Принцип приближения: Аппроксимация основана на идее приближения сложной функции или явления более простой моделью. Приближенные модели и функции обладают меньшей сложностью и проще описывают реальность. Они позволяют получить достаточно точные результаты без необходимости учета всех нюансов и деталей исследуемой системы.

3. Принцип адаптации: Аппроксимация может быть основана на принципе адаптации, который заключается в том, чтобы методически менять и уточнять модель, чтобы она лучше соответствовала реальным наблюдениям и данных. При адаптации модели корректируются параметры и структура модели, чтобы минимизировать разницу между предсказаниями модели и экспериментальными данными.

4. Принцип экономии: Аппроксимация позволяет сэкономить ресурсы, такие как время, усилия и вычислительную мощность, путем замены сложного явления или функции более простой моделью

Это особенно важно при изучении сложных и многоаспектных систем, где полное описание требует значительных ресурсов

5. Принцип проверки: Аппроксимация должна быть проверена путем сравнения результатов приближения с реальными наблюдениями или экспериментальными данными. Это позволяет оценить точность и надежность приближенной модели и ее применимость в реальных ситуациях. Принцип проверки помогает убедиться, что аппроксимация достаточно точна и применима перед дальнейшим использованием.

Принципы аппроксимации играют важную роль в науке, так как позволяют упростить сложные явления и функции, сэкономить ресурсы и получить приемлемую точность при анализе и прогнозировании. Аппроксимация широко применяется в различных областях и помогает исследователям лучше понять реальность и улучшить наши способности анализировать и предсказывать сложные системы и явления.

Качество аппроксимации данных

Качество аппроксимации данных является одним из важнейших факторов при выборе метода аппроксимации. Оно определяет степень точности, с которой аппроксимационная функция приближает исходные данные.

Важно понимать, что качество аппроксимации зависит не только от выбранного метода, но и от свойств исходных данных. Если данные имеют мало шумов и погрешностей, то качество аппроксимации может быть высоким

Однако, если исходные данные содержат большое количество шумов или выбросов, то точность аппроксимации будет ниже.

Существуют различные метрики для оценки качества аппроксимации данных. Одной из наиболее распространенных метрик является среднеквадратичная ошибка (MSE). Она вычисляется как среднее значение квадрата разности между значениями исходных данных и значениями аппроксимационной функции.

Кроме MSE, существуют также другие метрики, как, например, средняя абсолютная ошибка (MAE), коэффициент детерминации (R^2) и другие. Каждая метрика имеет свои преимущества и недостатки, и выбор конкретной метрики зависит от задачи и предпочтений исследователя.

Важно отметить, что качество аппроксимации данных не является абсолютным показателем, а скорее отражает степень приближения аппроксимационной функцией исходных данных. В зависимости от конкретной задачи и требований, можно выбирать различные методы аппроксимации и оценивать их качество с помощью соответствующих метрик

В общем случае, чем меньше значение выбранной метрики, тем лучше качество аппроксимации данных. Однако, необходимо учитывать и другие факторы, такие как структура аппроксимационной функции, сложность метода и его применимость к конкретной задаче.

Аппроксимация. «Ближнее», как Проксима Центавра

Если говорить простыми словами, аппроксимация — это нахождение ближнего. В математике это построение кривых, близких к имеющемуся набору значений. Представьте себе изменение показателя: оно строится по множеству найденных точек. Получается неровный, угловатый график, ведь при нахождении каждой точки были погрешности.

Например, точки — показания, снятые с какого-то датчика. На точность могут влиять помехи и разные шумы вокруг. Даже если результат двух измерений на самом деле одинаковый, датчик может выдать для них два разных результата из-за помех.

В таких ситуациях нужно сгладить график — найти средние значения, чтобы привести набор результатов к единой функции. Для этого существует аппроксимация функции. 

Пример аппроксимации по точкам:

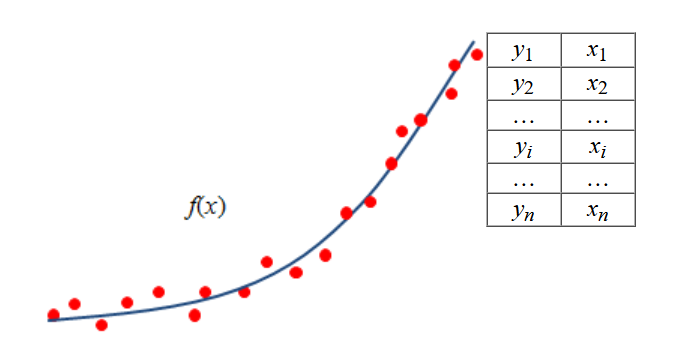
Красные точки на графике — найденные результаты. Они неоднородные, неровные, по ним не получится построить гладкую функцию. А синяя линия — линия аппроксимации. Она высчитана по аппроксимирующей функции f(x) и сделала результаты однороднее и проще для восприятия

Технически аппроксимация — это замена одних результатов другими, близкими к исходным, но упрощенными.

Зачем нужно. Компьютер может хранить данные со всеми неровностями и погрешностями, для него разницы нет. Но с информацией работает человек, а ему проще, когда набор данных можно описать функцией. Одна из задач науки о данных — прогнозирование. Если набор результатов можно описать функцией, прогнозировать легче. 

Как связано с другими методами. Методы аппроксимации помогают интерполировать и экстраполировать данные; об этом расскажем ниже. Аппроксимация — общий термин: интерполяция и экстраполяция считаются ее подвидами.

Станьте дата-сайентистом на курсе с МГУ и решайте амбициозные задачи с помощью нейросетей

Подробнее

Применение аппроксимации в астрономии

Аппроксимация — это методология, которая позволяет приближенно описывать сложные математические функции или процессы посредством более простых моделей или аппроксимирующих функций. В астрономии аппроксимация широко используется для анализа и предсказания различных астрономических явлений.

Одним из важнейших применений аппроксимации в астрономии является расчет орбит планет, космических аппаратов и других небесных тел. Орбиты характеризуются сложными математическими моделями, которые могут быть упрощены с помощью аппроксимации. Используя аппроксимацию, астрономы могут более точно предсказывать движение небесных тел и планировать космические миссии.

Другим применением аппроксимации в астрономии является анализ спектров звезд. Спектры звезд содержат множество линий поглощения и испускания, которые могут быть сложными для интерпретации. С помощью аппроксимации астрономы могут аппроксимировать спектральные линии с использованием известных моделей, что позволяет определить состав и физические характеристики звезды.

Другие задачи, в которых применяется аппроксимация, включают измерение расстояний между звездами и галактиками, моделирование гравитационных волн и оценку физических параметров космических объектов.

Важно отметить, что аппроксимация является лишь приближенным методом и может привести к неточностям в расчетах. Однако, благодаря аппроксимации астрономы могут получать более простые и удобные для анализа модели, что помогает сделать значительный прогресс в понимании и исследовании Вселенной

Аппроксимация в Excel статистических данных аналитической функцией.

Производственный участок изготавливает строительные металлоконструкции из листового и профильного металлопроката. Участок работает стабильно, заказы однотипные, численность рабочих колеблется незначительно. Есть данные о выпуске продукции за предыдущие 12 месяцев и о количестве переработанного в эти периоды времени металлопроката по группам: листы, двутавры, швеллеры, уголки, трубы круглые, профили прямоугольного сечения, круглый прокат. После предварительного анализа исходных данных возникло предположение, что  суммарный месячный выпуск металлоконструкций существенно зависит от количества уголков в заказах. Проверим это предположение.

Прежде всего, несколько слов об аппроксимации. Мы будем искать закон – аналитическую функцию, то есть функцию, заданную уравнением, которое лучше других описывает зависимость общего выпуска металлоконструкций от количества уголкового проката в выполненных заказах. Это и есть аппроксимация, а найденное уравнение называется аппроксимирующей функцией для исходной функции, заданной в виде таблицы.

1. Включаем Excel и помещаем на лист таблицу с данными статистики.

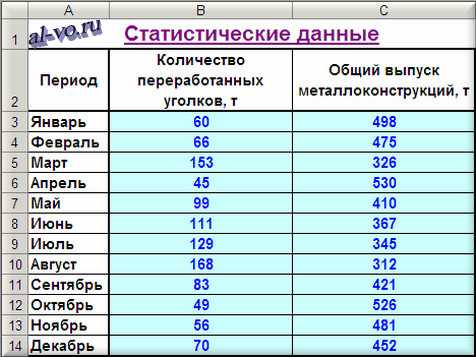
2. Далее строим и форматируем точечную диаграмму, в которой по оси X задаем значения аргумента – количество переработанных уголков в тоннах. По оси Y откладываем значения исходной функции – общий выпуск металлоконструкций в месяц, заданные таблицей.

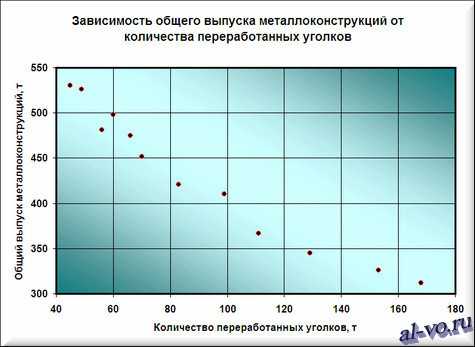
О том, как построить подобную диаграмму, подробно рассказано в статье «Как строить графики в Excel?».

3. «Наводим» мышь на любую из точек на графике и щелчком правой кнопки вызываем контекстное меню (как говорит один мой хороший товарищ — работая в незнакомой программе, когда не знаешь, что делать, чаще щелкай правой кнопкой мыши…). В выпавшем меню выбираем «Добавить линию тренда…».

4. В появившемся окне «Линия тренда» на вкладке «Тип» выбираем «Линейная».

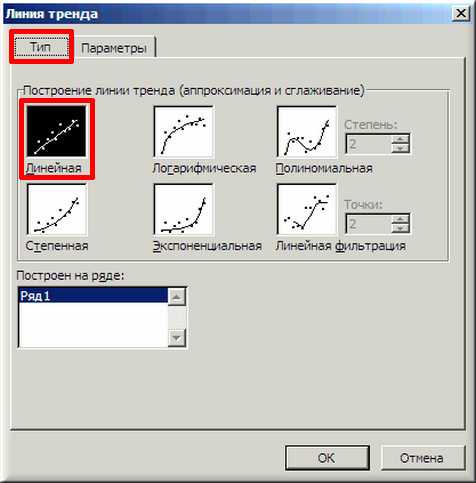
5. Далее на вкладке «Параметры» ставим 2 галочки и нажимаем «ОК».

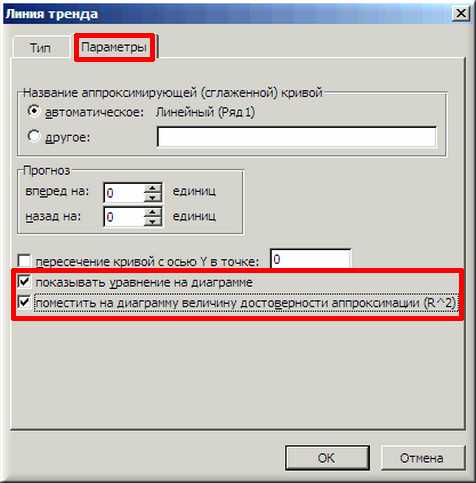
6. На графике появилась прямая линия, аппроксимирующая нашу табличную зависимость.

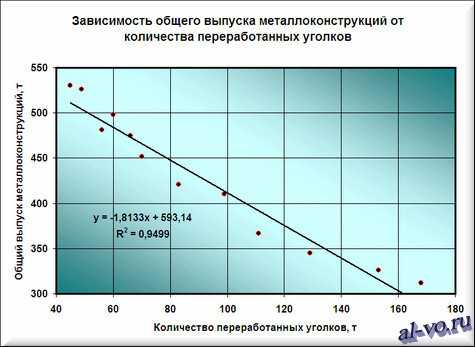
Мы видим кроме самой линии уравнение этой линии и, главное, мы видим значение параметра R2 – величины достоверности аппроксимации! Чем ближе его значение к 1, тем наиболее точно выбранная функция аппроксимирует табличные данные!

7. Строим линии тренда, используя степенную, логарифмическую, экспоненциальную и полиномиальную аппроксимации по аналогии с тем, как мы строили линейную линию тренда.

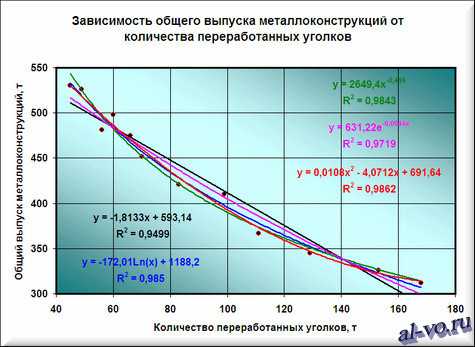
Лучше всех из выбранных функций аппроксимирует наши данные полином второй степени, у него максимальный коэффициент достоверности R2.

Однако хочу вас предостеречь! Если вы возьмете полиномы более высоких степеней, то, возможно, получите еще лучшие результаты, но кривые будут иметь замысловатый вид…

Здесь важно понимать, что мы ищем функцию, которая имеет физический смысл

Что это означает? Это означает, что нам нужна аппроксимирующая функция, которая будет выдавать адекватные результаты не только внутри рассматриваемого диапазона значений X, но и за его пределами, то есть ответит на вопрос: «Какой будет выпуск металлоконструкций при количестве переработанных за месяц уголков  меньше 45 и больше 168 тонн!» Поэтому я не рекомендую увлекаться полиномами высоких степеней, да и параболу (полином второй степени) выбирать осторожно!

Итак, нам необходимо выбрать функцию, которая не только хорошо интерполирует табличные данные в пределах диапазона значений X=45…168, но и допускает адекватную экстраполяцию за пределами этого диапазона. Я выбираю в данном случае логарифмическую функцию, хотя можно выбрать и линейную, как наиболее простую. В рассматриваемом примере при выборе линейной аппроксимации в excel ошибки будут больше, чем при выборе логарифмической, но не на много.

8. Удаляем все линии тренда с поля диаграммы, кроме логарифмической функции. Для этого щелкаем правой кнопкой мыши по ненужным линиям и в выпавшем контекстном меню выбираем «Очистить».

9. В завершении добавим к точкам табличных данных планки погрешностей. Для этого правой кнопкой мыши щелкаем на любой из точек на графике и в контекстном меню выбираем «Формат рядов данных…» и настраиваем данные на вкладке «Y-погрешности» так, как на рисунке ниже.

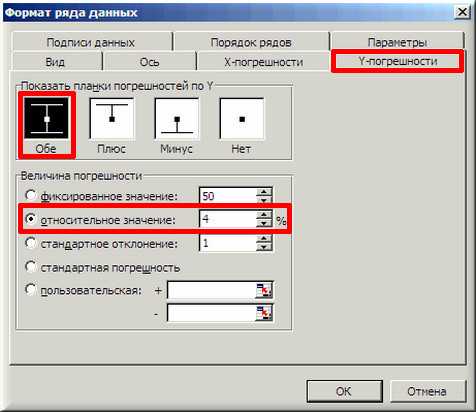
10. Затем щелкаем по любой из линий диапазонов погрешностей правой кнопкой мыши, выбираем в контекстном меню «Формат полос погрешностей…» и в окне «Формат планок погрешностей» на вкладке «Вид» настраиваем цвет и толщину линий.

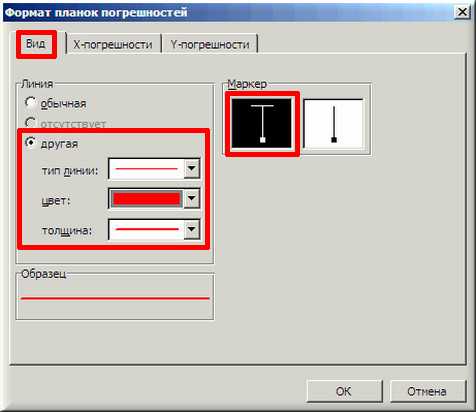
Аналогичным образом форматируются любые другие объекты диаграммы в Excel!

Окончательный результат диаграммы представлен на следующем снимке экрана.

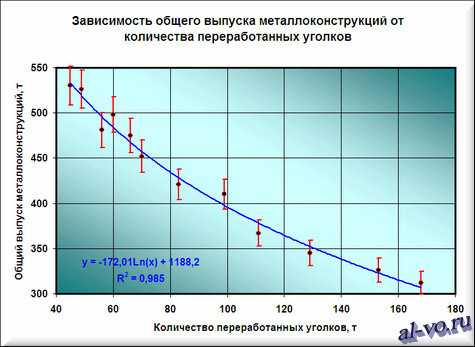
Аппроксимация

Относительно интерполяции, аппроксимация получила более широкое распространение. Сущность этого метода состоит в том, что табличные данные аппроксимируют кривой, которая не обязательно должна пройти через все узловые точки, а должна как бы сгладить все случайные помехи табличной функции.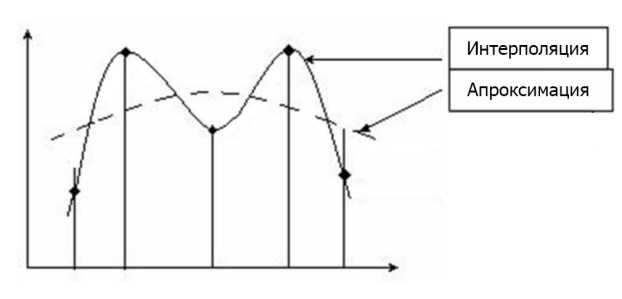

МНК (Метод Наименьших Квадратов)

Одним из самых популярных методов аппроксимации в Matlab и в других средах, это Метод Наименьших Квадратов ( МНК ). В этом методе при сглаживании опытных данных аппроксимирующую кривую стремятся провести так, чтобы её отклонения от табличных данных по всем узловым точкам были минимальными.

Суть МНК заключается в следующем: для табличных данных, полученных в результате эксперимента, отыскать аналитическую зависимость, сумма квадратов уклонений которой от табличных данных во всех узловых точках была бы минимальной.

Аппроксимация в Matlab по МНК осуществляется с помощью функции polyfit. Функция p = polyfit(x, y, n) находит коэффициенты полинома p(x) степени n, который аппроксимирует функцию y(x) в смысле метода наименьших квадратов. Выходом является строка p длины n+1, содержащая коэффициенты аппроксимирующего полинома.

Примеры задач

Разберём задачу, в которой разрешается использование встроенных матлабовских функций.

Осуществить аппроксимацию в Matlab табличных данных x = и y = . Применяя метод наименьших квадратов, приблизить ее многочленами 1-ой и 2-ой степени. Для каждого определить величину среднеквадратической ошибки. Построить (на одном листе) графики и заданной таблично функции (ломанная линия) и приближающих ее многочленов 1-ой и 2-ой степени.

x = 0, 0.1 , 0.2, 0.3, 0.5;
y = 3, 4.5, 1.7, 0.7, -1;
grid on
plot(x, y, '*r');
xi = min(x)0.1max(x);
N = 1; % степень
coeff1 = polyfit(x, y, N);
y2 = 0;
for k=0N
    y2 = y2 + coeff1(N-k+1) * xi.^k;
end
hold on; plot(xi, y2, 'r'); 
N = 2;
coeff2 = polyfit(x, y, N);
y3 = 0;
for k=0N
    y3 = y3 + coeff2(N-k+1) * xi.^k;
end
hold on; plot(xi, y3, 'g');
 
std(y-(coeff1(1)*x+coeff1(2)))
std(y-(coeff2(1)*x.^2+coeff2(2)*x+coeff2(3)))

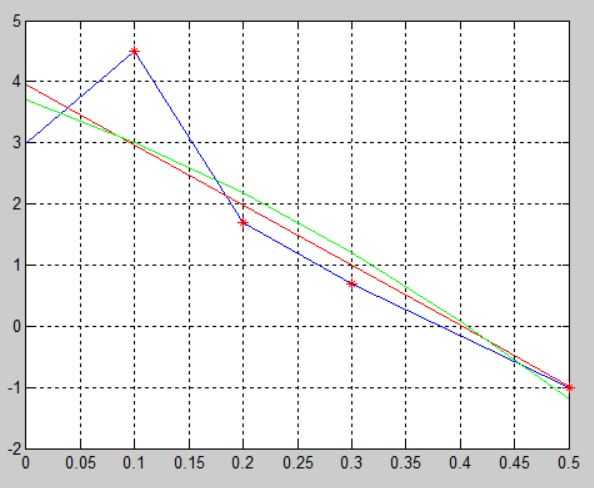Вывод:

Однако, встречаются задачи, где требуется реализовать аппроксимацию в Matlab без использования специальных функций. Найти у(0.25) путём построения аппроксимирующего полинома методом наименьших квадратов согласно данным: x: 0, 0.1, 0.2, 0.3, 0.5 y: 3, 4.5, 1.7, 0.7, -1 p: 0.5, 0.8, 1.6, 0.8, 0.1 Построить этот полином без учёта весовых коэффициентов с использованием определителя Вандермонда и стандартных операторов.

%Задаем массивы данных:
x = 0; 0.1; 0.2; 0.3; 0.5;
y = 3;4.5;1.7;0.7;-1;
%Строим матрицу W – матрицу Вандермонда с вырезанным первым столбцом:
W = vander(x);
W = W(15,25);
%Вычисляем элементы матрицы А как произведение транспонированной матрицы W и просто матрицы W
A = W'*W;
%Вычисляем элементы вектора b 
b = W'*y;
%Решая систему уравнений Aa = b, находим значения вектор-столбца a:
a = inv(A)*b
%Это будут коэффициенты аппроксимирующего полинома.
%Проверяем, используя методы MATLAB = функцию polyfit:
qq = polyfit(x,y,3)
%Получаем аппроксимированные значения y:
x1 = -0.20.0010.7;
y1 = a(1)*x1.^3 + a(2)*x1.^2 + a(3)*x1 + a(4);
%Строим график функции
plot(x,y,'*');
hold on;
grid on;
plot(x1,y1,'Color','r');
%Находим значение в точке x = 0.25
x2 = 0.25;
y2 = a(1)*x2^3 + a(2)*x2^2 + a(3)*x2 + a(4)

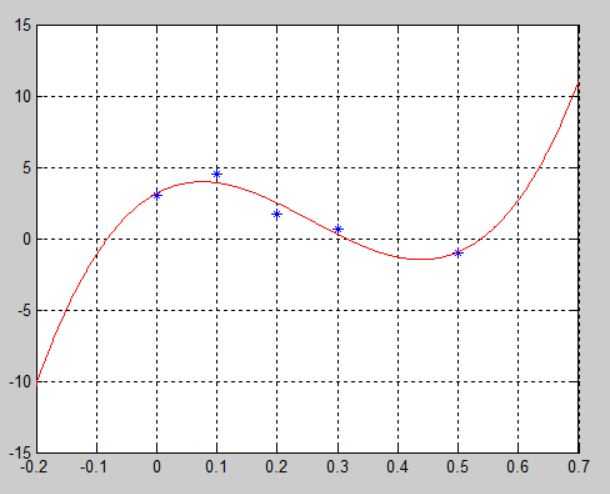Вывод:

Как видите встроенные функции для аппроксимации в Matlab укорачивают алгоритм почти вдвое.

Существует также возможность реализации всего алгоритма через одну функцию, но для преподавателей студентов она скорее всего будет не приемлема. С помощью функции lsqcurvefit(fun,x0,xdata,ydata), где:xdata,ydata– табличные значения аппроксимируемой функции;x0 –стартовое значение параметров функции;fun – функция аппроксимации, задаваемая пользователем

С аналитически-теоретической стороны, существуют такие виды аппроксимации:

• Аппроксимация ортогональными классическими полиномами.
• Аппроксимация каноническим полиномом

Но на практике их реализацию требуют редко.

Скачать исходник первой задачиСкачать исходник второй задачи

Как работает аппроксимация?

Аппроксимация — математический метод, позволяющий приближенно находить значение функции или набор данных. Она основана на замене исходной функции или набора данных более простой функцией или моделью, которая достаточно близка к исходной.

Основная идея аппроксимации заключается в том, чтобы выбрать наиболее подходящую функцию или модель для приближения исходных данных. Для этого используются различные методы и алгоритмы, которые позволяют определить оптимальные параметры для аппроксимирующей функции или модели.

Существует несколько основных типов аппроксимации:

• Полиномиальная аппроксимация — замена исходной функции полиномом определенной степени. Полиномы наиболее часто используются для аппроксимации функций вида f(x) = a + a₁x + a₂x2 + … + a_nxn. В зависимости от выбранной степени полинома, можно достичь различной точности аппроксимации.
• Интерполяционная аппроксимация — замена исходных данных интерполяционным полиномом, который точно проходит через все заданные точки. Этот метод позволяет получить точное значение функции в каждой из точек, но может привести к сильным колебаниям значения функции между точками, особенно при большом количестве точек.
• Нелинейная аппроксимация — замена исходной функции или данных нелинейной моделью, которая может быть более гибкой и точной, чем простые полиномы. Для поиска оптимальных параметров в нелинейной модели, используются методы оптимизации, такие как метод наименьших квадратов.

Перед проведением аппроксимации необходимо внимательно анализировать исходные данные, выбирать подходящую модель аппроксимации и контролировать точность результатов. Аппроксимация является одним из наиболее широко применяемых методов в математике и науке, и нашла свое применение в таких областях, как физика, экономика, статистика и многие другие.

Итоги.

Результатом всех предыдущих действий стала полученная формула аппроксимирующей функции y=-172,01*ln (x)+1188,2. Зная ее, и количество уголков в месячном наборе работ, можно с высокой степенью вероятности (±4% — смотри планки погрешностей) спрогнозировать общий выпуск металлоконструкций за месяц! Например, если в плане на месяц 140 тонн уголков, то общий выпуск, скорее всего, при прочих равных составит 338±14 тонн.

Для повышения достоверности аппроксимации статистических данных должно быть много. Двенадцать пар значений – это маловато.

Из практики скажу, что хорошим результатом следует считать нахождение аппроксимирующей функции с коэффициентом достоверности R2>0,87. Отличный результат – при  R2>0,94.

На практике бывает трудно выделить один самый главный  определяющий фактор (в нашем примере – масса переработанных за месяц уголков), но если постараться, то в каждой конкретной задаче его всегда можно найти! Конечно, общий выпуск продукции за месяц реально зависит от сотни факторов, для учета которых необходимы существенные трудозатраты нормировщиков и других специалистов. Только результат все равно будет приблизительным! Так стоит ли нести затраты, если есть гораздо более дешевое математическое моделирование!

В этой статье я лишь прикоснулся к верхушке айсберга под названием сбор, обработка и практическое использование статистических данных. О том удалось, или нет, мне расшевелить ваш интерес к этой теме, надеюсь узнать из комментариев и рейтинга статьи в поисковиках.

Затронутый вопрос аппроксимации функции одной переменной имеет широкое практическое применение в разных сферах жизни. Но гораздо большее применение имеет решение задачи аппроксимации функции нескольких независимых переменных…. Об этом и не только читайте в следующих статьях на блоге.

С интересом прочту Ваши комментарии, уважаемые читатели! Пишите!